Wavelet transforms in SkiaSharp
Previously, I wrote about frequency filtering an image using a Fast Fourier Transform. I implemented a band-pass filter, which attenuates very low and very high frequencies, but retains a middle band of frequencies. This technique is often used to enhance edges while reducing noise.
In this blog post I’ll discuss implementing a wavelet transform in SkiaSharp, to perform image upscaling and adaptive sharpening.
Wavelet transforms
I’m not going to explain what a wavelet transform is. Wikipedia, and other websites, take care of that adequately. What I will say though, is that wavelet transforms are pretty complicated. You need a thorough understanding of maths and signal processing before you can even begin to “grok” them.
Traditionally, wavelet transforms are used for signal/image/video compression, as they are fantastic for decomposing data into different frequency components at different levels of resolution. However, they can also be used for image upscaling, and adaptive sharpening. This blog post will focus on using a wavelet transform to perform image upscaling. For information about performing adaptive sharpening using a wavelet transform, see the implementation.
Implementing a wavelet transform
The wavelet transform algorithm that I implemented, which re-uses code going back to my C++ days, includes implementations of the Haar wavelet and the biorthoonal 5/3 wavelet. In both cases, the algorithm is capable of tranforming images of arbitrary sizes, not just powers of 2. In addition, the biorthogonal 5/3 wavelet implementation uses the lifting scheme (which is a second-generation wavelet transform). The lifting scheme speeds up the wavelet transform by factorising the transform into convolution operators, known as lifting steps, which reduce the number of arithmetic operations by nearly a factor of two.
The following code example shows a high level overview of the wavelet image upscaling process:
public static unsafe SKPixmap WaveletUpscale(this SKBitmap bitmap, Wavelet wavelet)
{
int width = bitmap.Width;
int height = bitmap.Height;
int upscaledWidth = width * 2;
int upscaledHeight = height * 2;
float[,] y = new float[upscaledWidth, upscaledHeight];
float[,] cb = new float[upscaledWidth, upscaledHeight];
float[,] cr = new float[upscaledWidth, upscaledHeight];
float[,] a = new float[upscaledWidth, upscaledHeight];
bitmap.ToYCbCrAArrays(y, cb, cr, a);
WaveletTransform2D wavelet2D;
WaveletTransform2D upscaledWavelet2D;
switch (wavelet)
{
case Wavelet.Haar:
wavelet2D = new HaarWavelet2D(width, height);
upscaledWavelet2D = new HaarWavelet2D(upscaledWidth, upscaledHeight);
break;
case Wavelet.Biorthogonal53:
default:
wavelet2D = new Biorthogonal53Wavelet2D(width, height);
upscaledWavelet2D = new Biorthogonal53Wavelet2D(upscaledWidth, upscaledHeight);
break;
}
wavelet2D.Transform2D(y);
wavelet2D.Transform2D(cb);
wavelet2D.Transform2D(cr);
wavelet2D.Transform2D(a);
upscaledWavelet2D.ReverseTransform2D(y);
upscaledWavelet2D.ReverseTransform2D(cb);
upscaledWavelet2D.ReverseTransform2D(cr);
upscaledWavelet2D.ReverseTransform2D(a);
for (int row = 0; row < upscaledHeight; row++)
{
for (int col = 0; col < upscaledWidth; col++)
{
y[col, row] *= 4.0f;
cb[col, row] *= 4.0f;
cr[col, row] *= 4.0f;
a[col, row] *= 4.0f;
}
}
SKImageInfo info = new SKImageInfo(upscaledWidth, upscaledHeight, SKColorType.Rgba8888);
SKImage image = SKImage.Create(info);
SKBitmap output = SKBitmap.FromImage(image);
SKPixmap pixmap = output.ToRGBAPixmap(y, cb, cr, a);
return pixmap;
}
The WaveletUpscale method is an extension method that works on SKBitmap objects, and requires a Wavelet argument that specifies which wavelet to use. This method doubles the width and height of the source image (although this could be parameterised if required). The image data is first converted from the RGBA colour space to the YCbCrA colour space, and its the data from this colour space that’s wavelet transformed using the supplied wavelet. The following image shows the Y channel from a wavelet transformed version of an image:
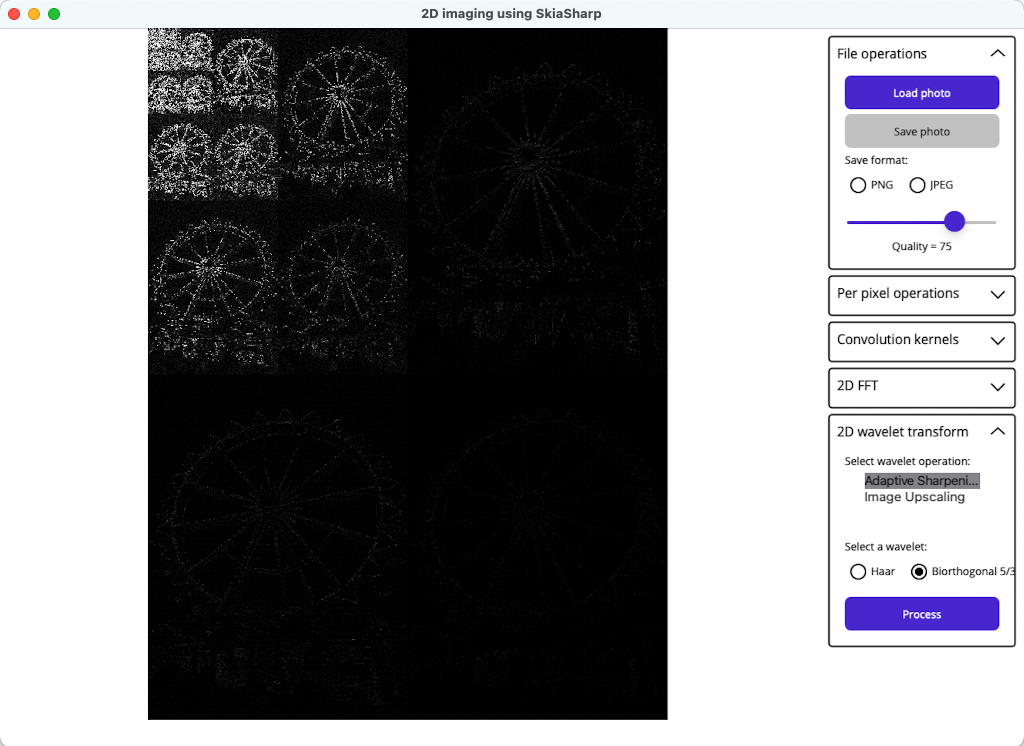
After the wavelet transform has been performed, the image data is in the frequency domain. If this data were reverse transformed, it would yield the original YCbCrA image data. However, here the frequency domain data is inverse transformed into an image of twice the size. A consequence of doing this is that the resulting YCbCrA data needs multiplying by a constant to return it to its correct form. This data is then converted back from the YCbCrA colour space to the RGBA colour space, for display.
This simple technique yields compelling results. I haven’t included any images showing the result because images taken using mobile devices already have a high resolution, which is then double by this process. It takes a lot of zooming into the image to see the detail achieved by the upscaling process. There’s no blockiness introduced. Instead, any artefacts are of the type commonly found in wavelet-based compression schemes. This technique could be further improved by performing different interpolation techniques to the data in the frequency domain, rather than simply inverse transforming the data into an image of twice the size.
Note: I’ve not included any wavelet transform code in this blog post, as it’s quite extensive. However, the main things to note are that: (1) it uses the Parallel.For loop to take advantage of multi-core processors, (2) it uses the lifting scheme to reduce the number of arithmetic operations performed, and (3) the code could be further optimised so that multiple passes of the data aren’t required.
While consumer imaging apps don’t typically contain operations that wavelet transform image data, it’s a mainstay of scientific imaging. It’s safe to say that SkiaSharp is a great framework for producing both consumer and scientific imaging apps, particularly cross-platform apps.