Performing convolution in SkiaSharp
Previously, I wrote about using SkiaSharp to obtain the pixel data for an image, and then manipulate the pixel data. SkiaSharp offers a number of different approaches for accessing pixel data. I went with the most performant approach for doing this, which is to use the GetPixels method to return a pointer to the pixel data, dereference the pointer whenever you want to read/write a pixel value, and use pointer arithmetic to move the pointer to other pixels.
In this blog post I’ll discuss performing convolution in SkiaSharp.
Implementing convolution
In image processing, convolution is the process of adding each element of an image to its local neighbours, weighted by a convolution kernel. The kernel is a small matrix that defines the imaging operation, such as blurring, sharpening, embossing, edge detection, and more. For more information about convolution, see Kernel image processing.
The ConvolutionKernels class in the app defines a number of kernels that each implement a different imaging operation, when convolved with an image. The following code shows three kernels from this class:
public class ConvolutionKernels
{
public static float[] EdgeDetection => new float[9]
{
-1, -1, -1,
-1, 8, -1,
-1, -1, -1
};
public static float[] LaplacianOfGaussian => new float[25]
{
0, 0, -1, 0, 0,
0, -1, -2, -1, 0,
-1, -2, 16, -2, -1,
0, -1, -2, -1, 0,
0, 0, -1, 0, 0
};
public static float[] Emboss => new float[9]
{
-2, -1, 0,
-1, 1, 1,
0, 1, 2
};
}
I implemented my own convolution method that performed convolution using 3x3 kernels and was reasonably happy with its execution speed. However, my ConvolutionKernels class includes kernels of different sizes, and so I had to extend the method to handle NxN sized kernels. Unfortunately, for larger kernel sizes the execution speed slowed dramatically. This is because convolution has a complexity of O(N2). However, there are fast convolution algorithms that reduce the complexity to O(N log N). For more information, see Convolution theorem.
Calling SkiaSharp’s convolution method
At this point SkiaSharp came to the rescue, courtesy of the CreateMatrixConvolution method in the SKImageFilter class. This method allows you to specify kernels of arbitrary size, allows you to specify how edge pixels in the image are handled, and is lightning fast.
The following code example shows how convolution is performed using this method:
void PerformConvolution()
{
float[] kernel = GetConvolutionKernel();
int length = kernel.Length;
int size = (int)Math.Sqrt(length);
SKSizeI sizeI = new SKSizeI(size, size);
SKPaint paint = new SKPaint()
{
IsAntialias = false,
IsDither = false
};
paint.ImageFilter = SKImageFilter.CreateMatrixConvolution(sizeI, kernel, 1f, 0f, new SKPointI(1, 1), SKShaderTileMode.Clamp, false);
_bitmapService.Paint = paint;
_bitmapService.InvalidateSurface();
}
The PerformConvolution creates an SKPaint object that will perform convolution when drawing an image to the screen. Importantly, the SKPaint object sets its ImageFilter property to the SKImageFilter object returned by the CreateMatrixConvolution method. The arguments to CreateMatrixConvolution are:
- The kernel size in pixels, as a
SKSizeIstruct. - The image processing kernel, as a
float[]. - A scale factor applied to pixel after convolution, as a
float. A value of 1 indicates that no scaling is applied. - A bias factor factor added to each pixel after convolution, as a
float. A value of 0 represents no bias factor. - A kernel offset, which is applied to each pixel before convolution, as a
SKPointIstruct. A value of 1,1 ensures that no offset values are applied. - A tile mode that represents how pixel accesses outside the image are treated, as a
SKShaderTileModeenumeration value. A value ofClampspecifies that the convolution should be clamped to the image’s edge pixels. - A
boolvalue that indicates whether the alpha channel should be included in the convolution.Falseensures that only the RGB channels are processed.
Note: Additional arguments for the CreateMatrixConvolution method can be specified, but aren’t required here. For example, you could choose to perform convolution only on a specified region in the image.
The SKPaint object is then set as the value of the Paint property on the BitmapRendererService object and the image is forcibly re-drawn with the call to InvalidateSurface. This causes the PaintSurface method to be invoked in the BitmapRendererSurface class:
SKBitmap _bitmap;
SKPaint _paint;
public void PaintSurface(SKSurface surface, SKImageInfo info)
{
SKCanvas canvas = surface.Canvas;
canvas.Clear();
if (_bitmap != null && _paint != null)
{
// Used for drawing the result of convolution operations
canvas.DrawBitmap(_bitmap, info.Rect, ImageStretch.Uniform, paint: _paint);
SKImage image = surface.Snapshot();
_bitmap = SKBitmap.FromImage(image);
_pixmap = _bitmap.PeekPixels();
_paint = null;
}
...
}
Provided that the BitmapRendererSurface.Paint property isn’t null, the image is re-drawn using the SKPaint object. This is what causes convolution to be performed with the chosen kernel. Therefore, the image that’s drawn on the screen will be the result of performing convolution on the source image. At this point, only the image that’s drawn on screen has the result of performing convolution with the chosen kernel, and so the PaintSurface method takes a snapshot of it, stores it as an SKBitmap, and stores a pointer to its pixel data. This is so that other imaging operations in the app can run on the convolution result. For information about the BitmapRendererService, see SkiaSharp and MVVM.
Watch out! Calling SKSurface.Snapshot isn’t ideal in this scenario because the resulting image will be the size of the surface, rather than the original image dimensions.
The following screenshot shows the result of performing convolution with the edge detection kernel:
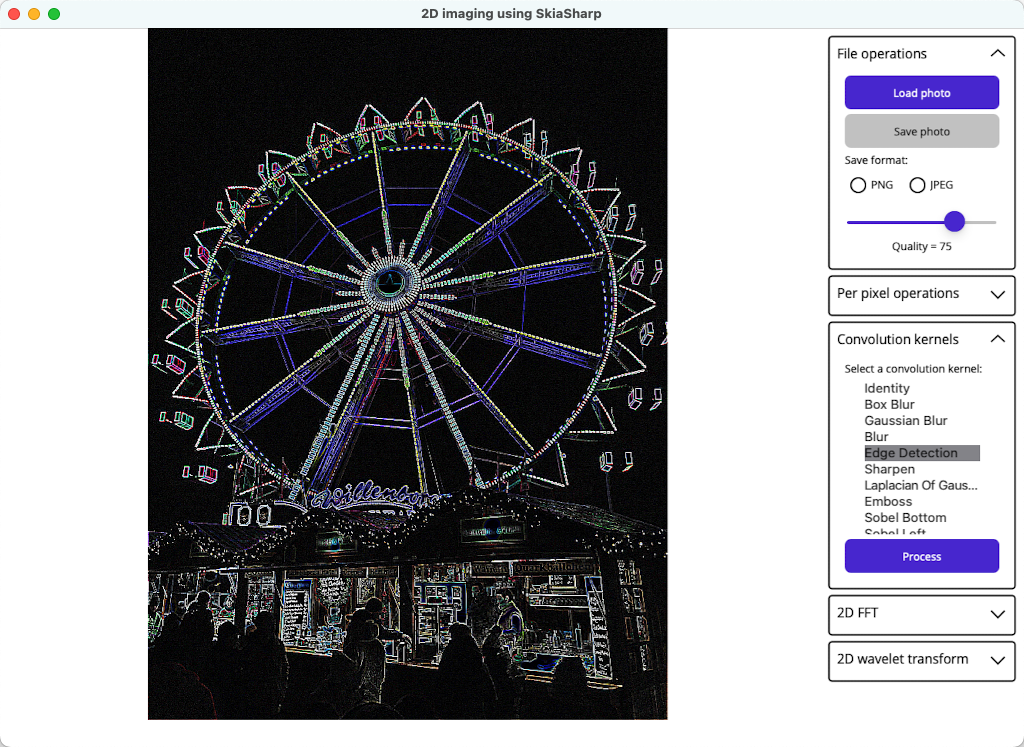
Note: The LaplacianOfGaussian kernel produces similar results to the EdgeDetection kernel. The difference is that the LaplacianOfGaussian kernel performs edge detection on smoothed image data. The Laplacian operator highlights regions of rapidy intensity change, and is applied to an image that has first been smoothed with a Gaussian smoothing filter in order to reduce its sensitivity to noise.
If you want to see other examples of using SkiaSharp in .NET MAUI, check out the SkiaSharp samples that I wrote while I was still at Microsoft.